FÓRMULA DO CONSUMO DE ELETRODOS EM FORNOS A ARCO

Luis R. Jaccard

Foi comprovado em laboratório e na prática que o consumo de ponta dos eletrodos, por unidade de tempo, é proporcional ao quadrado da corrente:

( Isto é bastante lógico, porque coincide com a fórmula da potência gerada em um resistor: P = I² x R ).

Com base na fórmula anterior e na seguinte figura é possível deduzir a fórmula do consumo específico de eletrodos.

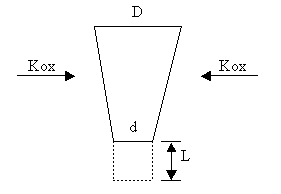
Figura 1 - Conicidade do eletrodo provocada por oxidação lateral

Em primeiro lugar há de ser considerado que o eletrodo depois de um certo tempo adquire o perfil da figura 1. O eletrodo vai-se afinando a medida que chega à ponta devido à oxidação lateral. A porção de grafita que está em determinado momento na ponta do eletrodo já esteve algumas horas ( ou dias ) antes na parte superior do mesmo e sofreu durante todo esse tempo um desgaste lateral que diminuiu o diâmetro de D para d. Apesar que a oxidação está desgastando o eletrodo, o consumo efetivo só vai ser computado a medida que o comprimento do eletrodo diminua ( exceto no caso que o eletrodo sem circulação de corrente permaneça tanto tempo dentro do forno como para se consumir totalmente em forma lateral, o que seria um caso irreal ).

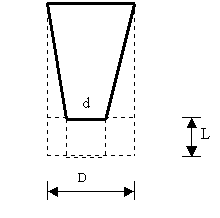
Apesar que o eletrodo se está consumindo pela ponta com um peso proporcional a d², o consumo real computado, cada vez que o comprimento L com diâmetro d é consumido, é proporcional a D² ( porque o que interessa é que foi gasto um comprimento L do eletrodo original de diâmetro D ).

Quer dizer, o eletrodo se consome com uma velocidade que é inversamente proporcional ao diâmetro da ponta "d", mas, quanto maior é a oxidação lateral, menor é "d" e, portanto, para um determinado valor de corrente, maior é a velocidade de consumo.

Ou seja, o consumo total de eletrodo por unidade de tempo será proporcional à densidade do material do eletrodo e ao volume de eletrodo de diâmetro D consumido em um certo tempo T ( peso de eletrodo consumido por unidade de tempo ).

Por outro lado, o consumo de ponta do eletrodo é proporcional a d²:

A partir de ( 2 ) e ( 3 ) chega-se à conclusão, mais ou menos óbvia, que o consumo total de eletrodos é igual ao consumo de ponta multiplicado por D² / d².

Mas, de acordo com ( 1 ), o consumo de ponta é proporcional a I² e, portanto:

Onde se chega à importante conclusão que o consumo de eletrodos em quilogramas por unidade de tempo é proporcional ao quadrado da corrente e à relação entre a seção original do eletrodo e a seção da ponta.

Interessa encontrar a equação que representa o consumo específico de eletrodos ( kg/t ), o qual consegue-se recordando que a produtividade do forno ( t/h ) é proporcional à potência ativa ( kW ) e inversamente proporcional ao consumo específico de energia elétrica Qee ( kWh/t ).

Trata-se da produtividade referida ao tempo de forno ligado ( quando realmente ocorre o consumo de ponta ). O consumo específico de eletrodos, em quilogramas de eletrodo por tonelada de aço produzida, será igual ao consumo de eletrodos por hora, dividido pelas toneladas produzidas em uma hora ( equação ( 5 ) dividida por (6 ) ).

Esta é a fórmula final do consumo de eletrodos. Na mesma pode-se ver que o consumo de eletrodos não tem qualquer relação com o tempo tap to tap ( D² / d² não depende do tempo tap to tap ).

O consumo específico de eletrodos é proporcional à relação entre o quadrado da corrente e a potência ativa, à conicidade do eletrodo e, ao consumo específico de energia elétrica.

O consumo específico de eletrodos em quilogramas por kWh consumido é igual a:

Para poder aplicar as equações ( 7 ) e ( 8 ) é necessário saber como D²/d² varia em função dos outros parâmetros.

Pode ser demonstrada a seguinte correlação entre a conicidade do eletrodo, os parâmetros de operação e as características do forno ( ver artigo completo sobre a equação do consumo de eletrodos ):

Onde H é a altura de oxidação do eletrodo ( parte vermelha do eletrodo ).

Conclui-se que a conicidade do eletrodo e, portanto, o consumo específico de eletrodos é tanto maior quanto menor é a densidade de corrente no eletrodo.

Substituindo ( 9 ) en ( 8 ):

A anterior é a fórmula final do consumo específico de eletrodos.

Partindo de esta fórmula podem-se extrair interessantes conclusões práticas:

1. O consumo de ponta e, em geral, o consumo total de eletrodos é tanto menor quanto menor é a relação I² / P. Mas, I² / P é proporcional a P / Va² = I / Va = 1 / Ra. Ou seja, para determinada potência ativa, o consumo de eletrodos é inversamente proporcional à tensão de arco ao quadrado. Também se observa que o consumo de eletrodos sempre é inversamente proporcional à resistência do arco. No caso de fornos de arco submerso pode ser substituída a resistência de arco pela resistência elétrica da carga e, a tensão de arco pode ser substituída pela tensão eletrodo-soleira.

2. O consumo por oxidação, que é o que aumenta a conicidade do eletrodo, depende da relação entre a área de oxidação e o quadrado da corrente ( D x H / I² ). Este aspecto é muito interessante porque mostra que apesar de normalmente ocorrer uma forte diminuição do consumo de eletrodos ao diminuir a corrente, em certos casos extremos ( fornos operando com muito baixa densidade de corrente no eletrodo ) uma diminuição da corrente pode provocar um aumento de consumo total. Também conclui-se que a utilização de eletrodos de diâmetro superior ao necessário provoca um aumento do consumo.

APLICAÇÃO PRÁTICA DA EQUAÇÃO DO CONSUMO DE ELETRODOS

Ultimamente, em forma prática, encontramos algumas constantes que substituídas na equação ( 10 ) permitiram obter valores de consumos de eletrodos bastante próximos dos reais, em diferentes fornos de arco direto:

São utilizadas as seguintes unidades:

I ( kA ); Va ( V ) ; D ( cm ); H ( m )

Exemplo:

D = 60 cm
I = 80 kA
Va = 625 V [ Va é igual a P_1eletrodo ( kW ) / I ( kA )]
H = 2,2 m

Resultado:

Ce´= 2,62 kg / MWh

APLIQUE A FÓRMULA PARA O CASO DOS SEUS FORNOS E ENTRE EM CONTATO CONOSCO !!!

VOLTAR À HOME PAGE